ULTRAFAST SPECTROSCOPY: RECENT PROGRESS AND CHALLENGES
Section n. 1
Broadband laser sources for ultrafast spectroscopy
Written by Vasilis Petropoulos (ESR5)
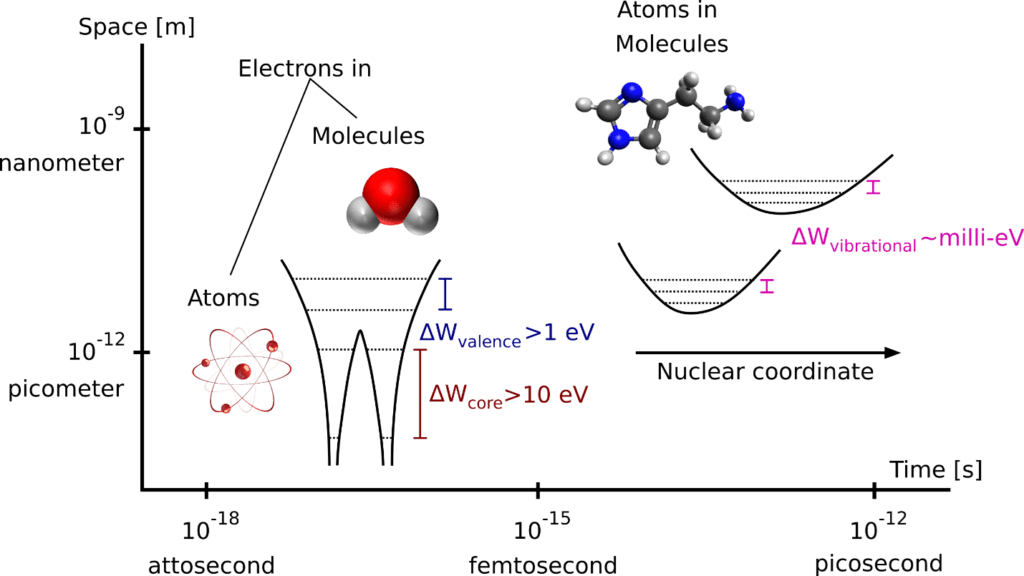
The physical properties of Nature at the scale of atoms and subatomic particles are governed by quantum mechanics. Assuming that a subatomic particle is in a superposition of states, so-called wave packet, between two states with energies W1, W2, the wave function of the particle has an oscillatory solution, between these two states, from Schrödinger equation with period: Tosc = 2π(ℏ/∆W), where ∆W= W2 – W1 [1]. In order to resolve molecular vibrations of a molecule, as the wave packet oscillates between vibrational states having an energy gap around meV (Figure 1), time resolution of tens to hundreds of femtoseconds (fs) is needed. Similarly, to capture the motion of individual electrons in molecular orbitals and inner shells of atoms (Figure 1), time resolution ranging from tens of femtoseconds (fs) to less than an attosecond (as) is required. The need of ultrashort pulses (fs- to as durations) to study molecular and electronic motions during physical phenomena, led to the birth of femto-chemistry [2], and more recently to the atto-chemistry [1] fields.
Ultrafast optical spectroscopy uses sequences of ultrashort light pulses to track ultrafast photoinduced dynamical processes. Recent progress in theory [3, 4] and technology [5] raised the need to seek for more sophisticated techniques beyond the commonly used ‘pump-probe’ technique, exploring multi-dimensional approaches that can increase the amount of information.
Ultrashort light sources can be generated and tuned in a wide spectral range. Furthermore, to yield an experimental sensitivity (e.g. high signal to noise ratio), light sources functioning at high repetition rates while scaling high average powers too, are optimal.
The two main primary solid-state sources of ultrashort pulses are Ti:sapphire lasers and Yb:doped crystal or fiber lasers. Ti:sapphire lasers have 800 nm output wavelength and can provide 50-100 fs ultrashort pulses. Yb:doped lasers have 1030 nm output wavelength with longer pulse widths (150-300 fs) but able to operate in high repetition rates [6]. The advantages of these primary laser sources are their stability and reliability, with the major drawback that they operate at fixed wavelengths, with limited tuning capabilities. Although, they can act as driving pulses to create secondary sources by nonlinear conversion processes. Optical parametric amplification (OPA) is a second-order nonlinear effect that can generate broadly tunable Fourier-limited pulses, spanning from the visible till the infrared. Additional second-order nonlinear processes, like second-harmonic generation (SHG), sum-frequency generation (SFG), difference-frequency generation (DFG) and optical rectification enable the extension to wider spectral ranges. SHG and SFG allow the generation of ultrashort light sources in the ultraviolet region, while DFG and optical rectification enable the accomplishment of mid-infrared and Terahertz regions, respectively [6]. These spectral ranges are essential in order to study electronic and vibrational molecular dynamics governing photoinduced chemical processes and electronic interactions in the excited state, as well as structural dynamics of molecular systems in their electronic ground state, respectively.
Extreme-ultraviolet (XUV) coherent light pulses with durations of tens of attoseconds can be produced using high-order harmonic generation (HHG), focusing high-intensity femtosecond pulses onto noble gases. Attosecond light sources can be generated either in the form of isolated pulses or trains of pulses separated by half an optical cycle of the driving pulse [1]. However, isolated attosecond pulses, required for attosecond spectroscopy, operate with low pulse energies which has delayed advanced time-resolved measurements [7].
Theoretical calculations by Mukamel highlight the importance of performing multidimensional spectroscopies using X-ray pulses [4]. Femtosecond hard X-ray pulses in a laser-driven source is based on vacuum accelerated electrons, on the time scale of the optical cycle of the driving laser pulse, focusing onto metal atoms in the target. Inner-shell ionization of metal atoms followed by spontaneous emission of an outer shell electron into the unoccupied inner shell, emits characteristic X-ray lines [8]. In addition to optical spectroscopies, the use of X-ray sources for ultrafast diffraction techniques, can spatially resolve electron density maps with a resolution of a fraction of a chemical bond length, as a function of time.
Source | Wavelength | Pulse width | Pulse energy | Repetition rate |
Primary solid-state lasers | ||||
Ti:sapphire | 800 nm | 50-100 fs | 1-10 mJ | 1 Hz-200 kHz |
Yb laser | 1030 nm | 150-300 fs | 10 μJ-1 mJ | 1 kHz-10 MHz |
Secondary sources by nonlinear frequency conversion | ||||
X-ray through inner-shell ionization of metal atoms
| 0.01-10 nm | » 100 fs | Depends on the accelerated electrons | 1Hz-1KHz |
Attosecond XUV Through Noble gases | 10-125 nm | 70–320 as | 1 pJ- 10 nJ | Depends on the driving pulse |
SHG, SFG | 200-400 nm | 10-200 fs | 0.1-1 μJ | 1-200 kHz |
Yb-pumped OPA | 390-3000 nm | 5-200 fs | 1-100 μJ | 1 kHz-10 MHz |
Ti:sapphire-pumped OPA | 450-3000 nm | 5-100 fs | 1 μJ-1 mJ | 1-200 kHz |
DFG | 3-15 μm | 30-200 fs | 0.1-10 μJ | 1-200 kHz |
Terahertz through optical rectification | 150-600 μm | » 1 ps | 0.1 nJ-1 μJ | 1 kHz-100 MHz |
The primary and secondary laser sources discussed above in terms of wavelength, pulse width, energy and repetition rate, are summarized in Table 1 in ascending operating-wavelength order. An ideal ultrabroadband, high peak power and few-cycle light pulse source could be achieved by synthesizing multiple laser sources. At this moment, in the range of visible till mid-infrared, the most prominent technology for producing such an ideal source is the optical parametric chirped pulse amplification (OPCPA) [9]. OPCPA is based on the coherent combination of carrier-envelope-phase-stable pulses that emerge from different optical parametric amplifiers. Extending the idea of coherent wavelength multiplexing for shorter wavelengths to produce ultrabroadband ideal laser sources awaits to be applied. However, an ultrabroadband source with the above-mentioned ideal characteristics is not trivial to be manipulated in order to perform ultrafast optical measurements. The development of an ideal ultrabroadband source from laser technology will raise a wealth of technical challenges.
The continuous progress in laser technology along with technical advances and conceptual breakthroughs, expand the application potential of Ultrafast Spectroscopy. Nowadays, we are closer than ever to turn state of the art ultrafast spectroscopic techniques into a laboratory routine. The access to sophisticated techniques with few-cycle light pulses and for wide spectral ranges, can bring us closer to the grand goal of tracking the motions of electrons and molecules in space and time with unprecedented resolution.
Section n. 2
Pulse shaping techniques for ultrafast spectroscopy
Written by Vikramdeep Singh (ESR2)
In light-matter interaction studies involving investigations of quantum coherent processes and non-linear optical processes, ultrafast short optical pulses of picosecond and femtosecond time scales are generated routinely nowadays. The most common approach to generate ultrafast short pulses in the deep femtosecond regime is by using mode locked lasers. Another approach is based on using electro-optic modulation and subsequent compression of continuous wave lasers. Using high order nonlinear frequency conversion processes even attosecond pulses can be attained. There are broad applications for ultrafast short pulses involving ultrafast spectroscopy, nonlinear microscopy, and laser machining. Ultrafast broadband Fourier limited laser pulses are used to attain sufficient time resolution to give insights into the dynamics of ultrafast quantum processes. To control this interaction, control over the temporal pulse shape is required, which is provided by pulse shaping technologies. Pulse shaping techniques provide user-defined ultrafast optical waveforms with control over phase, amplitude, and polarization of the pulses. User-controlled pulse waveforms have applications in ultrafast spectroscopy, spectrally selective non-linear microscopy, tracing of electronic coherences using multi-dimensional spectroscopy, and other applications including few cycle pulse compression, dispersion compensation for fibre optic communications, and coherent control of quantum mechanical processes. Inherent phase stability of the time delayed pulses created in the pulse shaper simplifies multi-dimensional spectroscopy experiments. The primary focus of this section is to give a brief introduction about the femtosecond programmable pulse shaping techniques used in multidimensional spectroscopy.
Pulse shaping in multidimensional spectroscopy
In multidimensional spectroscopy techniques e.g., 2D electron spectroscopy, early-stage experiments were limited by phase-stability issues, since phase locked pump pulses are required for doing Fourier transform of the non-linear signal. To counter the phase stability issues, passive phase stabilization approaches were used initially, where phase-locked two pump pulses were generated by using diffractive optics or beam splitters. Using interferometric techniques for phase-locked pulses pair generation is suitable for two pulse experiments however in case of three pulse sequences it becomes more difficult and thus pulse shaping is a suited choice. 2DES in UV and visible spectral region using passive birefringent interferometer for generation of phase locked pump pulse pair is demonstrated in [10,11]. In addition to this, the delay time between the pulses is usually set by increasing the optical path length for the pulse. It is realized by using either piezoelectric delay stages with retroreflective optics or by changing amount of material the pulse passes through e.g., wedged optics. Translating Wedge based Identical pulse eNcoding System (TWINS) which uses birefringence property to generate phase-locked pulses with very high precise time delays is employed in 2DUV and visible spectroscopy [10,11]. Such moving or translation mechanics can take up to 50-100ms during which data cannot be collected and thus increases the data acquisition times. In shot-to-shot experiments, such as molecular dynamics studies, pulse shapers can play a big role in making data acquisition more rapid as there are no moving mechanics. Pump-probe and 2D electron spectroscopy studies have proven that data acquisition rate and signal to noise ratio is enhanced using high repetition rate laser pulses, specifically the data collection rate increases linearly with repetition rates. With high waveform refresh rates in pulse shapers rapid data acquisition and precise delay is achievable. On the contrary, dead time in translational stages cannot be reduced significantly. Rapid data collection in 2DIR and visible spectroscopy using partially collinear geometry and a pulse shaper to generate time dependent amplitudes and arbitrary control over the phase is reported in [12]. Several groups have demonstrated techniques where entire 2D spectra can be recorded in single laser shot without the need of physical time delay mechanism. A 2DES variant technique gradient-assisted photon echo spectroscopy (GRAPES) in which pulses are cylindrically focussed and by relative tilt of the pump pulses waveforms, time delay is encoded in vertical dimension on the sample. In this scheme, 2D spectra is obtained for every laser shot and thus reduces the acquisition times nominally. The only requirement is to have a sample which is spatially homogeneous over a millimetre size range [13].
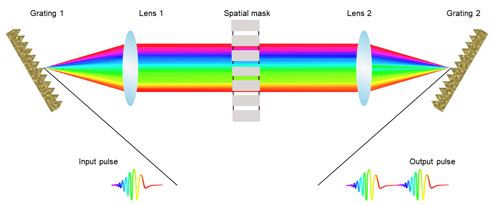
Different pulse shaping techniques
The most general approach used for pulse shaping is Fourier filtering of the ultrafast optical pulses using a 4-f geometry set-up, this scheme is termed as Fourier transform pulse shaping [14]. In 4-f geometry setup, the main components are pair of grating, two cylindrical lenses, and a spatial mask. The optical frequency spectrum of an input laser pulse is spatially dispersed using grating over the spatial mask. There are many different techniques developed and applied for spatial masking e.g., using different spatial light modulators- acousto-optic modulators (AOM) and liquid crystal modulator (LCM), former preferred for rapid refresh rates, the latter for higher resolution. The intensity and phase of the laser pulses are manipulated using the AOM and LCM as spatial masks in the Fourier plane of the 4-f geometry [15]. The condition for time-invariant filtering is that the AOM refresh rate should be higher than pulse repetition rate. A good example of programmable pulse shaping technique to generate user-defined optical wavefronts is by using acousto-optic programmable dispersive filter (AOPDF) [16]. The birefringent properties of the acousto-optic crystal for optical and acoustic waves are utilized. A transient grating is generated by the acoustic waves which shapes the optical pulse by diffracting the ordinary incoming optical wave into different extraordinary optical waves thus attaining the pulse shaping by anisotropic interaction.
There are other approaches reported, using digital mirror device (DMD) as spatial mask. A thin strip of several hundred thousand microscopic mirrors, with each pixel serving as binary mirror with on-off states. This device is programmed with phase modulation patterns which masks on a spatially spread input pulse [17]. The advantage of using DMD based ultrafast pulse shapers is that they can be used with high repetition rate laser pulse with refresh rates up to 2MHz as compared to AOMs which have refresh rate of 100KHz. DMD are also cost effective compared to AOM or LCM and operate at high frame rates over broad range from UV to IR using appropriate coating [18]. DMD enabled pulse shapers are limited by their low efficiency and are typically used in combination of chirped pulse amplifiers. AOM pulse shapers with very high repetition rate of 10MHz are reported taking advantage of the Fourier shift theorem [19]. Recently, using dielectric metasurfaces as spatial mask in a 4-f geometry setup, pulse shaping of near IR is achieved [20]. The spectrum is dispersed into two spatial dimensions which would increase the individually controllable spectral features by several orders of magnitude as two-dimensional wavefront shapers.
Section n. 3
Resources for improving data acquisition and coherence characterization in ultrafast spectroscopy
Written by Frank Quintela (ESR12)
Eliminating heat-induced signals by controlling pulse spectra through pulse shaping
Nonlinear spectroscopy involves the interaction of a system with multiple light pulses at variable times, to reconstruct the system’s response signal. To isolate the third-order contribution, a “chopping” strategy is standard in pump-probe spectroscopy, were one of the pulses is alternatively blocked, causing the nonlinear signal to switch off/on [5].
The environment (“bath”) of the system is modeled as a mode continuum, composed by a combination of intramolecular and intermolecular modes. Infrared light pulses produce short-lived vibrational excitations, resulting in a rapid deposition of heat into the bath. This generates unwanted heat signals by creating spectral shifts in the bath and system absorption [22]. As the linear response is typically many orders of magnitude higher than the third order nonlinear one, a minuscule change in the bath absorption spectrum, when “chopping” the pulse, can result in a differential heat signal on the same scale as the nonlinear signal.
The problem of unwanted heat signals was adressed in Ref. [21], which conducted experiments on the CN stretch of phenylselenocyanate (PhSeCN) in a dimethylformamide (DMF) solvent. Instead of “chopping”, they used a pulse shaper to selectively block the excitation of the system modes, while delivering the rest of the energy to the bath modes. Figure 3 shows this “pulse-shaping chopping” scenario. The strategy was tested by probing the relaxation of the CN stretch, which should follow a known single exponential decay if no bath modes are excited.
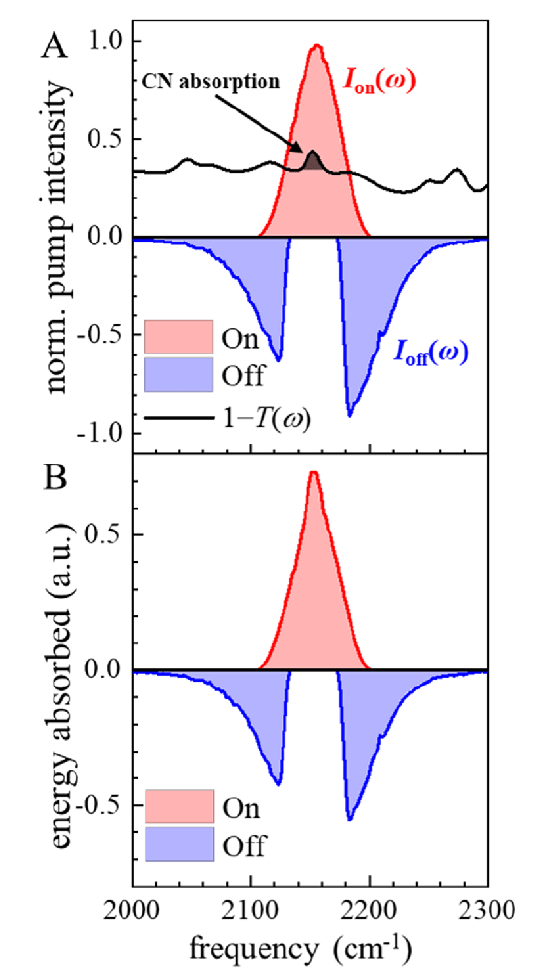
The method proved useful when the vibrational system absorption line is narrow compared to the pulses spectrum, and the on/off pulses are adjusted to match the energy delivered to the bath.
Interestingly, if the system is only excited with the spectrum shaped (Off) pulse, the dependence on the heat signals for the CN shows up, allowing to probe the system-bath coupling.
Compressive sensing to shorten the data acquisition time
Spectroscopic techniques possess an intrinsic trade-off between data-acquisition speed and measurement sensitivity. Repeating measurements reduces experimental noise and increases accuracy through an averaging process, but more time is then required to collect a full dataset. An ultrafast experiment ranges typically from several minutes to hours, depending on the technique used. Shortening measurement time guarantee laser stability and allows the examination of fragile specimens that quickly degrade during experiments. A measurement speed up becomes even more relevant when scaling to multidimensional spectroscopy.
Compressive sensing (CS) is a signal processing technique for efficiently acquiring and reconstructing signals. Resting on the assumption that the signal is sparse on some known basis [24], the number of required measurements could be reduced to M << N, where N is determined by the Nyquist-Shannon sampling theorem [25]. CS is suited for ultrafast optics because the system response is often dominated by a small number, or small range of frequencies, implying the existence of a sparse basis.
The signal reconstruction proceeds through solving the convex optimization problem
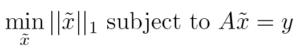
for x̃, with A=ϕψ⁻¹ the sensing matrix, ψ a known N x N matrix transforming to the sparse basis x̃ = ψx, ϕ a M x N random matrix, y the M-points measured signal [26]. Once x̃ is computed, it is transformed to a N-points signal x in the measurement basis, which is the CS estimate of the ultrafast signal.
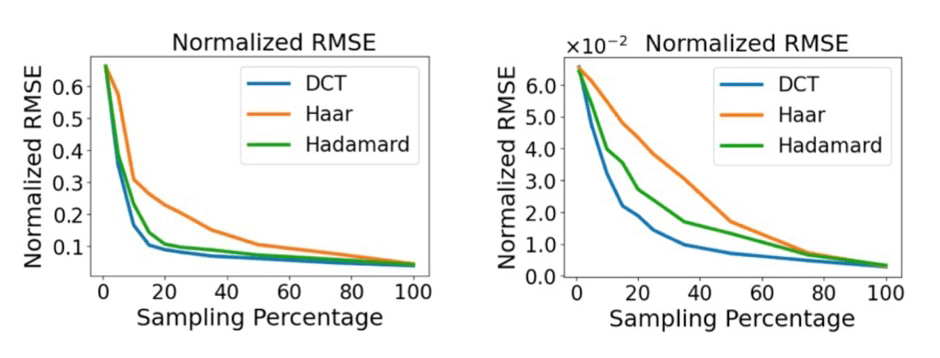
In Ref. [23], CS was tested on experimental data from ultrafast transient absorption (pump-probe) spectroscopy of broad plasmon band of the TiN nanoparticles, and ultrafast terahertz spectroscopy of a methylammonium lead iode (MAPbI₃) thin film on quartz. Figure 4 shows the normalized root-mean-square error as a function of the sampling percentage, when comparing complete measurements with the estimated ones, being ψ the Discrete Cosine (DCT), Haar and Hadamard transformations. Those results suggest that a sampling range of 15-25% gives a good estimate of the full signal.
This achieved speed up makes CS promissing. However, the procedure still rests on a number of ad hoc elements, i.e., the arbitrary choice of the sensing matrix, the determination of the suitable sampling and stopping criteria for the M samples. It has been proposed that, on long term, combining machine learning and CS would automatise the deduction of the appropriate transformations to deliver the required sparsity, and hence the best estimation [28].
Simultaneous frequency and time resolution using time-frequency transforms
In ultrafast spectroscopy the data are recorded both in time and frequency domains [6], the translation between them being achieved by numerical computation of the direct/inverse Fourier Transform (FT). The spectral domain allows the identification of the relevant frequencies, associated with the energy of the states involved in the coherent superposition [5], where higher amplitudes represent a dominant “time averaged”contribution. Multi-component transient signals, as often encountered in ultrafast experiments, result from the superposition of several beating components, each one characterized by different frequencies and time-dependent amplitudes. Many relevant physical phenomena (i.e., relaxation, exciton transfer) may be represented by those signals, the interpretation of which would require simultaneous time and frequency resolution, to detect how frequency contents change over time. This is, however, constrained by a known uncertainty relationship [29], rendering classical FT analysis unsuitable for this task.
Time-frequency transform (TFT) has been proposed to circumvent this limitation [30]. It consist in defining 2D-maps S(t,v) whose amplitude shows a correlation between t and v for the given signal. Some examples are presented below.
The Short-time Fourier Transform STFT, Eq. (2), examines the frequency content of the signal s(t’) as the window function h(t’-t) is moved along t, providing the FT only of the signal portion delimited by h,
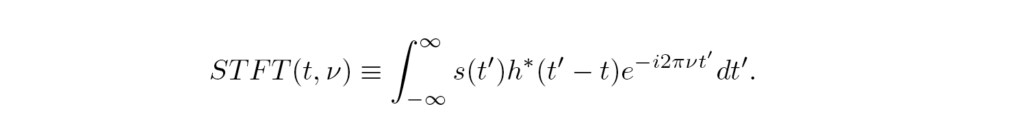
The Continuous wavelet transform CWT, Eq. (3), uses a short time oscillating function ψ called wavelet instead of a fixed window h(t). The transform amplitude gives, at each time t, higher values when the typical frequencies of the signal s(t’) match the frequency a,
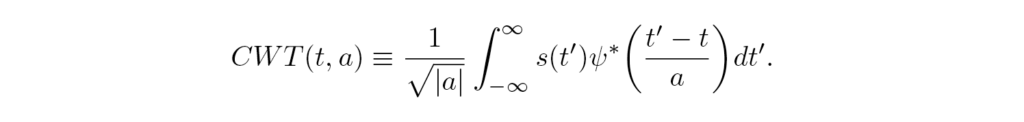
The Wigner-Ville distribution WV, Eq. (4), is the FT of the signal autocorrelation function with respect to the delay variable. Its frequency integration gives the modulus of the signal |s(t)|², while integration over time gives the energy spectrum |S(v)|². Its generalization using window functions h,g gives the smoothed-pseudo-Wigner-Ville distribution (SPWV), Eq. (5),
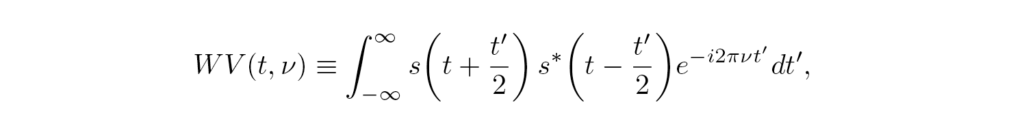
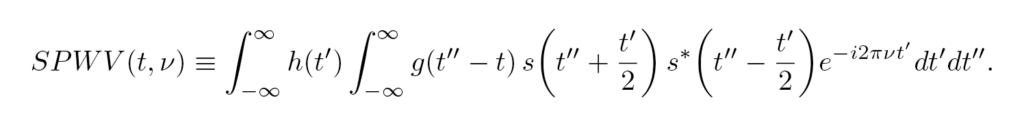
In Ref. [28], the performance of those and other transforms was tested with a reference signal, for which the lifetime of each frequency was known in advance. The results showed that most of those transforms are robust when signal noise is added, and are insensitive to the chosen window functions, for which using gaussians results convenient. However, the gaussian’s widths are still critical parameters for the analysis, leaving its choice to heuristic criteria depending on the target signal.
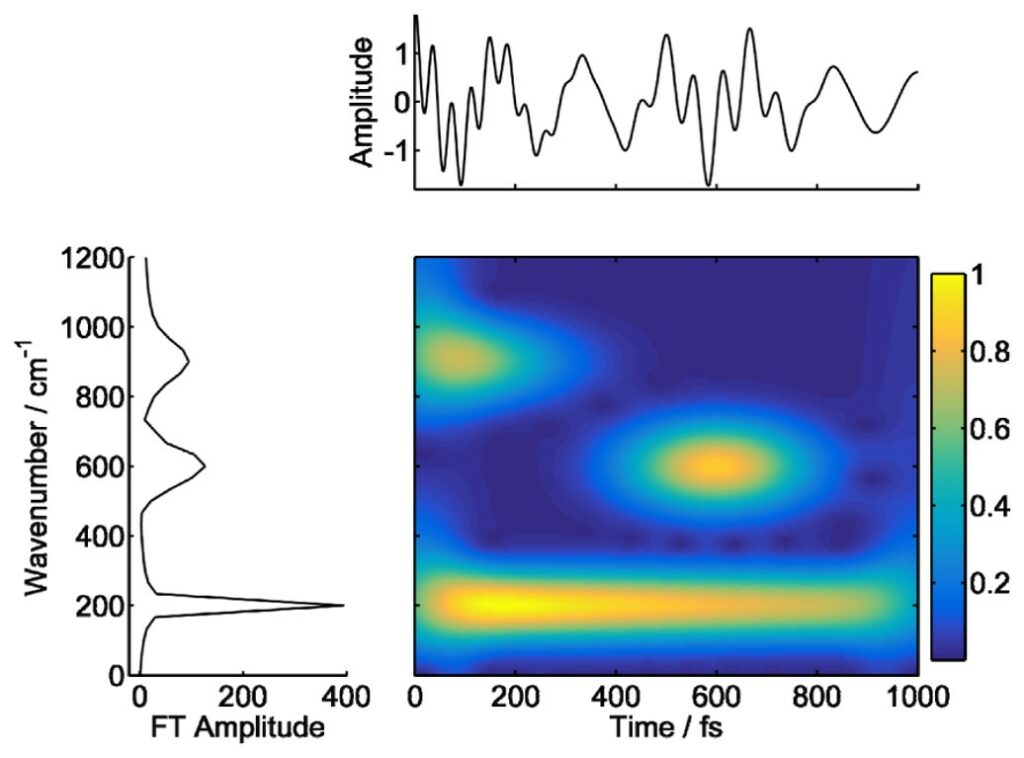
Figure 5 shows an example of TFT map. From the plot, the following can be addressed: 1. coherence characterization, through the observation of the lifetime of frequency signals, 2. the identification of energy transfer pathways, by following the activation/deactivation of frequencies over time. This makes TFT a valuable resource when studying ultrafast response in molecular systems.
About the Authors
The MUSIQ Innovation Newletter n.2 was written by three of the Early Stage Researchers (ESRs) working on individual projects as part of the MUSIQ project.

Vasilis Petropoulos (ESR5)
Vasilis is hosted at the Politecnico di Milano, Physics Department. His research there focuses in Ultrafast coherent spectroscopy of natural light-harvesting systems.

Vikramdeep Singh (ESR2)
Vikramdeep is hosted at Cardiff University at the School of Physics and Astronomy. His research project focuses on 2D FWM cryo-microspectroscopy of individual colloidal quantum dots, fluorophores, and biomolecules.

Frank Quintela (ESR12)
Frank is hosted at the Università degli Studi di Modena e Reggio Emilia and his research is on Simulating ultrafast coherent phenomena in model light-harvesting complexes.
References
[1] Krausz, F. & Ivanov, M. Attosecond physics. Rev. Mod. Phys. 81, 163–234 (2009).
[2] Zewail, A. H. Femtochemistry: Atomic-scale dynamics of the chemical bond. J. Phys. Chem. A 104, 5660–5694 (2000).
[3] Mukamel S 2000 Multidimensional Femtosecond Correlations Spectroscopies of Electronic and Vibrational Excitations Annu. Rev. Phys. Chem. 51 691–729.
[4] Kowalewski, M., Fingerhut, B. P., Dorfman, K. E., Bennett, K. & Mukamel, S. Simulating Coherent Multidimensional Spectroscopy of Nonadiabatic Molecular Processes: From the Infrared to the X-ray Regime. Chem. Rev. 117, 12165–12226 (2017).
[5] Hamm, P. & Zanni, M. Concepts and Methods of 2D Infrared Spectroscopy. (Cambridge University Press, 2011). doi:10.1017/CBO9780511675935.
[6] Maiuri, M., Garavelli, M. & Cerullo, G. Ultrafast Spectroscopy: State of the Art and Open Challenges. J. Am. Chem. Soc. 142, 3–15 (2020).
[7] Chini, M., Zhao, K. & Chang, Z. The generation, characterization and applications of broadband isolated attosecond pulses. Nat. Photonics 8, 178–186 (2014).
[8] Holtz, M. et al. Towards shot-noise limited diffraction experiments with table-top femtosecond hard x-ray sources. Struct. Dyn. 4, (2017).
[9] Moses, J., Manzoni, C., Huang, S.-W., Cerullo, G. & Kaertner, F. X. Temporal optimization of ultrabroadband high-energy OPCPA. Opt. Express 17, 5540 (2009).
[10] R. Borrego-Varillas, A. Oriana, L. Ganzer, A. Trifonov, I. Buchvarov, C. Manzoni, and G. Cerullo, Two-dimensional electronic spectroscopy in the ultraviolet by a birefringent delay line, Optics Express, 24, 25, 28491-28499, 2016.
[11] J. Réhault, M. Maiuri, A. Oriana, and G. Cerullo, Two-dimensional electronic spectroscopy with birefringent wedges, 85, 12, 123107, 2014.
[12] Sang-Hee Shim and Martin T. Zanni, How to turn your pump–probe instrument into a multidimensional spectrometer: 2D IR and Vis spectroscopies via pulse shaping, Phys. Chem. Chem. Phys., 11, 5, 748-761, 2009.
[13] E. Harel, and Andrew F. Fidler, and Gregory S. Engel, Single-Shot Gradient-Assisted Photon Echo Electronic Spectroscopy, The Journal of Physical Chemistry A, 115, 16, 3787-3796, 2011.
[14] A.M. Weiner, Femtosecond optical pulse shaping and processing, Prog. in Quantum Electron., 19, 3, 1995, 161-237, 1995.
[15] A.M. Weiner, Femtosecond pulse shaping using spatial light modulators, Rev. Sci. Instrum., 71, 5, 1929-1960, 2000.
[16] F. Verluise, V. Laude, Z. Cheng, Ch. Spielmann, and P. Tournois, Amplitude and phase control of ultrashort pulses by use of an acousto-optic programmable dispersive filter: pulse compression and shaping, Opt. Lett., 25, 575-577, 2000.
[17] C. Gu, Y. Chang, D. Zhang, J.Cheng, and S-C Chen, Femtosecond laser pulse shaping at megahertz rate via a digital micromirror device, Opt. Lett., 40, 4018-4021, 2015.
[18] C. Gu, D. Zhang, Y. Chang, and S-C Chen, Digital micromirror device-based ultrafast pulse shaping for femtosecond laser, Opt. Lett., 40, 2870-2873, 2015.
[19] S. Dinda, S. N. Bandyopadhyay, and D. Goswami, Rapid programmable pulse shaping of femtosecond pulses at MHz repetition rate, OSA Continuum, 2, 14, 1386-1400, 2019.
[20] S. Divitt, W. Zhu, C. Zhang, H. J. Lezec and A. Agrawal, Ultrafast optical pulse shaping using dielectric metasurfaces, Science, 364, 890—894, 2019.
[21] D. J. Hoffman, S. M. Fica-Contreras, J. Pan, and M. D. Fayer, Pulse-shaped chopping: Eliminating and characterizing heat effects in ultrafast infrared spectroscopy., J Chem Phys 153, 204201 (2020), https://doi.org/10.1063/5.0031581.
[22] L. De Marco, J. A. Fournier, M. Tha ̈mer, W. Carpenter, and A. Tokmakoff, Anharmonic exciton dynamics and energy dissipation in liquid water from two-dimensional infrared spectroscopy, The Journal of Chemical Physics 145, 094501 (2016), https://aip.scitation.org/doi/pdf/10.1063/1.4961752.
[23] S. Adhikari, C. L. Cortes, X. Wen, S. Panuganti, D. J. Gosztola, R. D. Schaller, G. P. Wiederrecht, and S. K. Gray, Accelerating ultrafast spectroscopy with compressive sensing, Physical Review Applied 15, 024032 (2021).
[24] Compressed Sensing: Theory and Applications (Cambridge University Press, 2012).
[25] N = 2fcT, where T is some maximum time required to observe the dynamics, fc the highest frequency of the signal.
[26] S. S. Chen, D. L. Donoho, and M. A. Saunders, Atomic decomposition by basis pursuit, SIAM review 43, 129 (2001).
[27] A. Bustin, N. Fuin, R. M. Botnar, and C. Prieto, From compressed-sensing to artificial intelligence-based cardiac mri reconstruction, Frontiers in Cardiovascular Medicine 7, 17 (2020).
[28] A. Volpato and E. Collini, Time-frequency methods for coherent spectroscopy, Optics express 23, 20040 (2015).
[29] D. Gabor, Theory of communication. part 1: The analysis of information, Journal of the Institution of Electrical Engineers- Part III: Radio and Communication Engineering 93, 429 (1946).
[30] L. Cohen, Time-frequency analysis, Vol. 778 (Prentice Hall PTR Englewood Cliffs, NJ, 1995).

